\(\mathrm{PSp}(4, \mathbb{R})\)

Let \(V\) be a vector space and let \(K\) be a field. A symplectic bilinear form on \(V\) is a bilinear map \(\omega : V\times V \to K\) such that \(\omega\) is

1. Alternating: \(\omega(u,u) = 0\) for all \(u \in V\);
2. Non-degenerate: \(\omega(u,v) = 0\) for all \(v \in V\) implies that \(u=0\).

A symplectic vector space is a vector space equipped with a symplectic bilinear form. Also, by fixing a basis, it's possible to represent the symplectic bilinear form \(\omega\) by a matrix \(\Omega\).

The symplectic group, denoted \(\mathrm{Sp}(2n, K)\), is the group of linear transformations of a symplectic \(K\)-vector space of dimension \(2n\) preserving the symplectic bilinear form. In our case, we are interested in the group \[\mathrm{Sp}(4, \mathbb{R}) = \{M \in M_{4}(\mathbb{R}) \mid M^{T}\Omega M = \Omega\},\] and more precisely by the projective symplectic group \[\mathrm{PSp}(4,\mathbb{R}) = \mathrm{Sp}(4,\mathbb{R})/\{-I,I\}.\] It is a group of \(10\) dimensions.

Let's consider the group of Möbius transformations \(\mathcal{Möb}\) as a subgroup of \(\mathrm{PGL}(4,\mathbb{R})\). This group is a subgroup of \(\mathrm{PSp}(4, \mathbb{R})\) of \(6\) dimensions. By parameterizing the \(4\) other dimensions with sliders, we obtain the entirety of \(\mathrm{PSp}(4, \mathbb{R})\). The Möbius transformations are selected the same way that is described in their dedicated section.

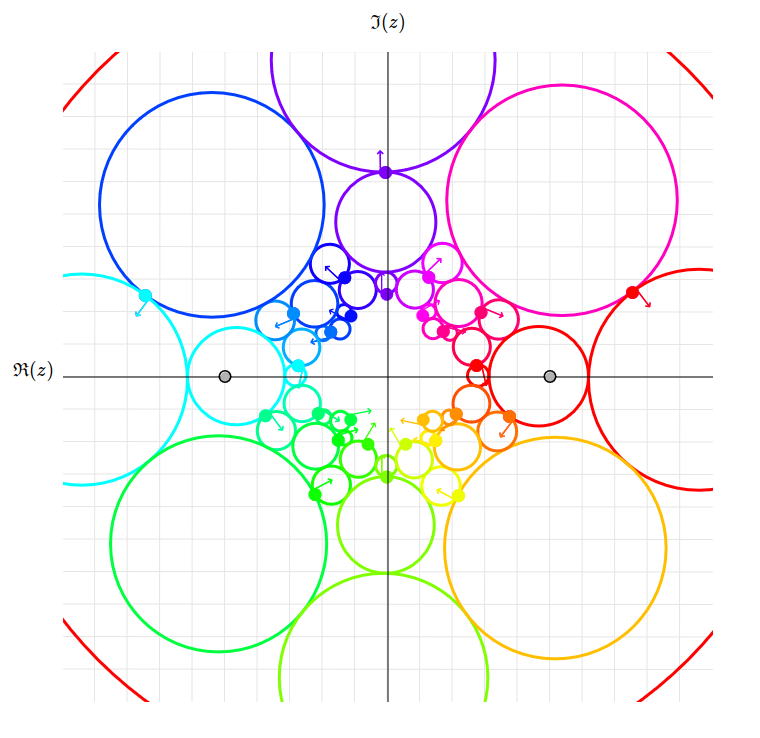
On the left, we visualise the action of \(\mathrm{PSp}(4, \mathbb{R})\) on isotropic flags (visualised as oriented circles with a point), and on the right, on the Veronese curve.