Soient \(V\) un espace vectoriel et \(K\) un corps. Une forme symplectique sur \(V\) est une application bilinéaire \(\omega : V\times V \to K\) telle que \(\omega\) est
Un espace vectoriel symplectique est un espace vectoriel muni d'une forme symplectique. De plus, en fixant une base, il est possible de représenter la forme symplectique \(\omega\) par une matrice \(\Omega\).
Le groupe symplectique, noté \(\mathrm{Sp}(2n, K)\), est le groupe des transformations linéaires d'un \(K\)-espace vectoriel symplectique de dimension \(2n\) préservant la forme symplectique. Dans notre cas, nous nous intéressons au groupe \[\mathrm{Sp}(4, \mathbb{R}) = \{M \in M_{4}(\mathbb{R}) \mid M^{T}\Omega M = \Omega\}\] et plus particulièrement, au groupe projectif symplectique \[\mathrm{PSp}(4,\mathbb{R}) = \mathrm{Sp}(4,\mathbb{R})/\{-I,I\}.\] C'est un groupe de \(10\) dimensions.
Considérons le groupe des transformations de Möbius \(\mathcal{Möb}\) en tant que sous-groupe de \(\mathrm{PGL}(4,\mathbb{R})\). Ce groupe est un sous-groupe de \(\mathrm{PSp}(4, \mathbb{R})\) de \(6\) dimensions. En paramétrant les \(4\) autres dimensions par des sliders, nous obtenons l'entièreté de \(\mathrm{PSp}(4, \mathbb{R})\). Les transformations de Möbius sont sélectionnées de la même façon que décrite dans leur section dédiée.
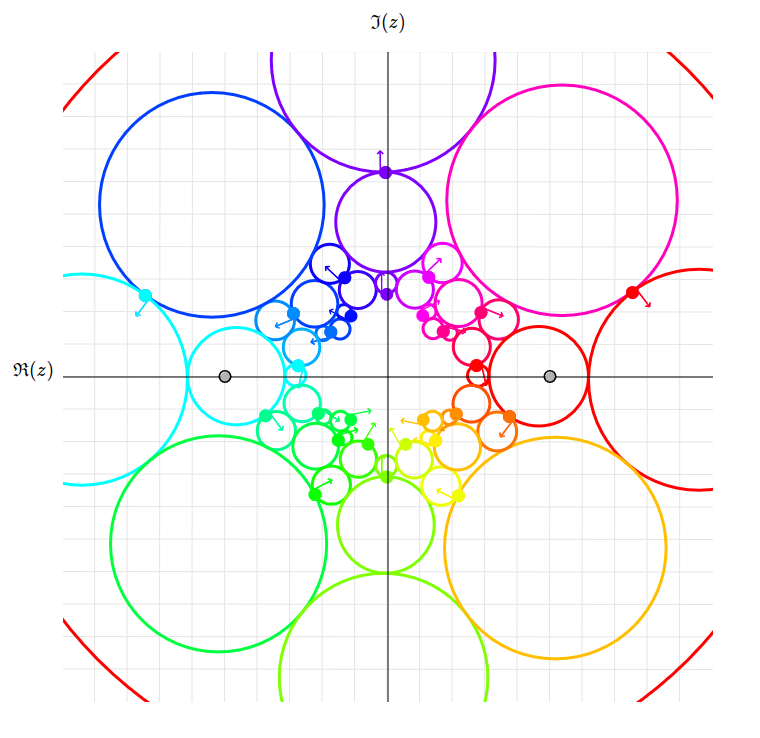
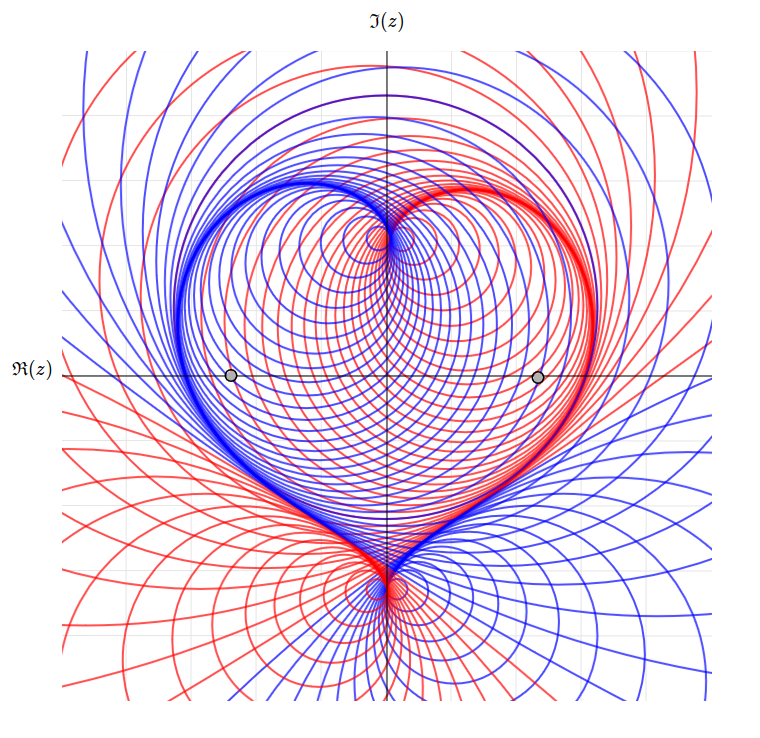
À gauche, nous visualisons l'action de \(\mathrm{PSp}(4, \mathbb{R})\) sur des drapeaux isotropes (visualisés en tant que cercles orientés avec point) et à droite, sur la courbe de Veronese.