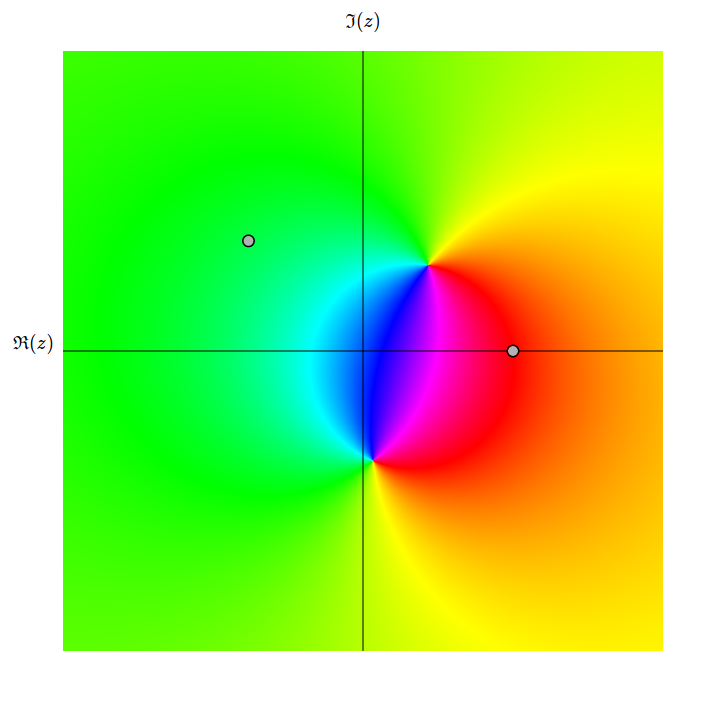
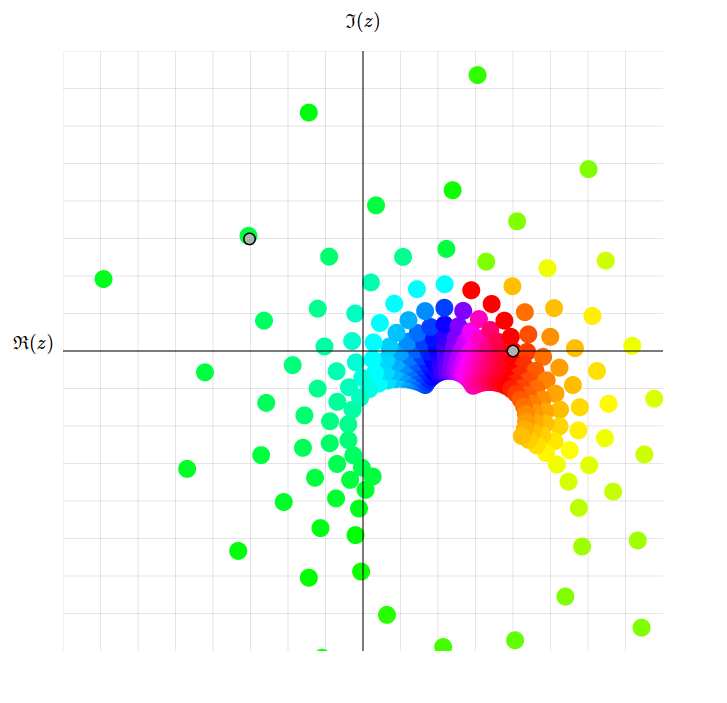
Une transformation de Möbius \(M\) est une fonction \(M: \hat{\mathbb{C}}\rightarrow\hat{\mathbb{C}}\), où
\(\hat{\mathbb{C}} = \mathbb{C}\cup\{\infty\}\) et est appelée la sphère de Riemann.
Plus précisément, une transformation de Möbius est une fonction définie par
\begin{align*}
M : \hat{\mathbb{C}} &\rightarrow \hat{\mathbb{C}}\\
z &\mapsto \frac{az+b}{cz+d}
\end{align*}
avec \(a,b,c,d \in \mathbb{C}\) et \(ad-bc \neq 0\).
Le programme utilise le fait qu'il existe une unique \(M\) telle que, pour \(\{z_{1},z_{2},z_{3}\}\) et \(\{w_{1},w_{2},w_{3}\}\)
deux ensembles d'éléments distincts dans \(\hat{\mathbb{C}}\), nous avons que \(M(z_{i}) = w_{i}\) pour \(i=1,2,3\).
Les deux points gris représentent \(z_{1} = w_{1}\) et \(z_{2} = w_{2}\) et en glissant la souris,
vous spécifiez \(z_{3} \mapsto w_{3}\). Le programme trouve alors la fonction \(M\) correspondante et applique la transformation sur la sphère de Riemann!
À gauche, la visualisation utilise du domain coloring et à droite, elle utilise des points discrets \(a+b\mathrm{i}\) avec \(a,b \in \mathbb{Z}\).