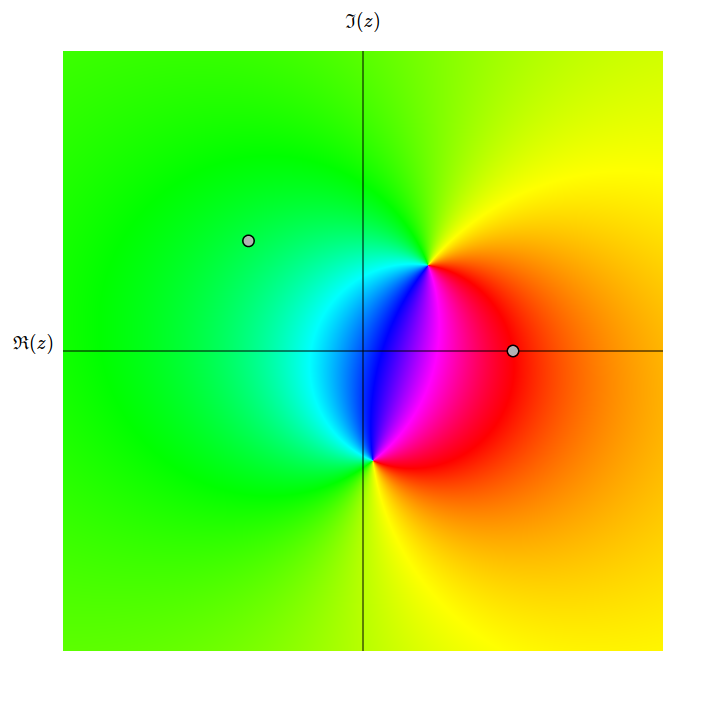
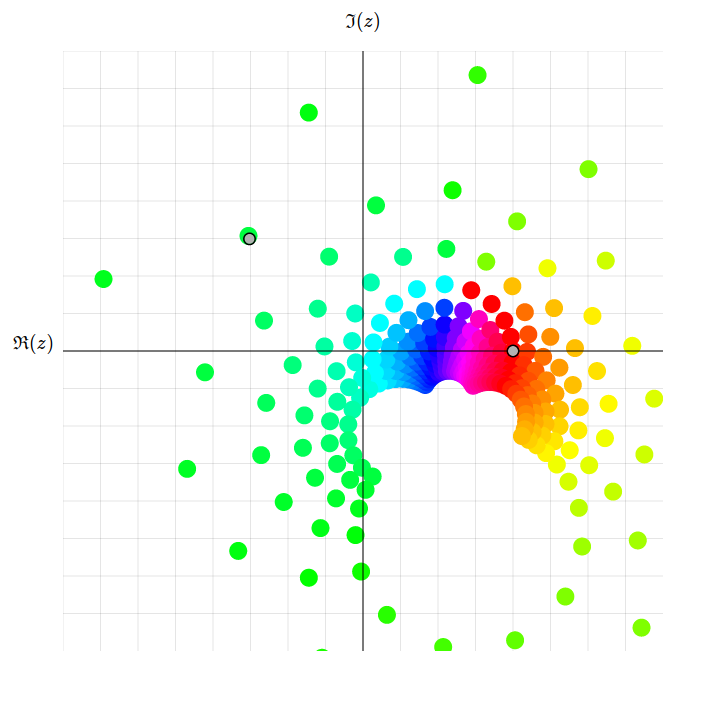
A Möbius transformation \(M\) is a function \(M: \hat{\mathbb{C}}\rightarrow\hat{\mathbb{C}}\), where
\(\hat{\mathbb{C}} = \mathbb{C}\cup\{\infty\}\) and is called the Riemann sphere.
More precisely, a Möbius transformation is a function defined by
\begin{align*}
M : \hat{\mathbb{C}} &\rightarrow \hat{\mathbb{C}}\\
z &\mapsto \frac{az+b}{cz+d}
\end{align*}
with \(a,b,c,d \in \mathbb{C}\) and \(ad-bc \neq 0\).
The following program uses the fact that
there exists a unique \(M\) such that for \(\{z_{1},z_{2},z_{3}\}\) and \(\{w_{1},w_{2},w_{3}\}\) two sets
of distinct elements in \(\hat{\mathbb{C}}\), we have
\(M(z_{i}) = w_{i}\) for \(i=1,2,3\).
The two grey points represent \(z_{1} = w_{1}\) and \(z_{2} = w_{2}\), and by dragging your mouse,
you specify \(z_{3} \mapsto w_{3}\). The program then finds the corresponding \(M\) and applies the transformation on the Riemann sphere!
On the left, the visualisation uses domain coloring, and on the right, it uses discrete points \(a+b\mathrm{i}\) with \(a,b \in \mathbb{Z}\).