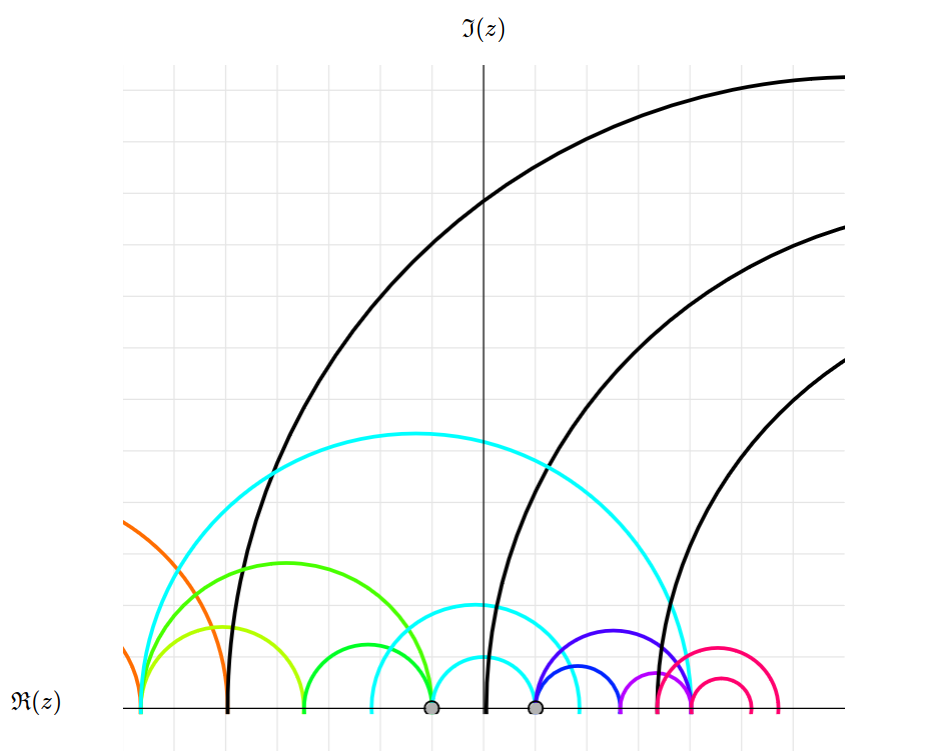
Ce site permet de voir l'action de \(\mathrm{PSL}(2,\mathbb{R})\) sur \(\mathbb{H}_{\mathrm{sup}} \coloneqq \{x+iy \in \mathbb{C} \mid y>0\}\), le demi-plan supérieur ou le demi-plan de Poincaré. L'action est une transformation de Möbius, c'est-à-dire que l'action est définie par \[\begin{pmatrix}a&b\\c&d\end{pmatrix}\cdot z = \frac{az+b}{cz+d},\] où \(z \in \mathbb{H}_{\mathrm{sup}}\) et \(a,b,c,d \in \mathbb{R}\) sont tels que \(ad-bc=1\).
Le fonctionnement du programme est basé sur le théorème suivant :
Classification des isométries. \(\mathrm{PSL}(2,\mathbb{R})\) est le groupe des isométries de \(\mathbb{H}_{\mathrm{sup}}\) préservant l'orientation.
De plus, une transformation satisfait exactement un de ces cas :
Le programme utilise le fait qu'étant donné un de ces cas, il existe une unique transformation qui envoie \(z_{1} \in \mathbb{H}_{\mathrm{sup}}\) à \(z_{2} \in \mathbb{H}_{\mathrm{sup}}\) ou \(x_{1} \in \mathbb{R}\cup\{\infty\}\) à \(x_{2} \in \mathbb{R}\cup\{\infty\}\), selon le cas où on se trouve. Les points gris représentent les points fixes. En glissant la souris, vous spécifiez \(z_{1} \mapsto z_{2}\) ou \(x_{1} \mapsto x_{2}\). Le programme différencie ces cas pour vous. Ensuite, il trouve l'unique transformation et l'applique aux droites hyperboliques!
Le site est grandement inspiré de celui fait pour visualiser l'action de \(\mathrm{PSP}(4,\mathbb{R})\) sur la sphère de Riemann. Le code relatif à ce site se trouve sur GitHub. Les visualisations ont été faites avec CindyJS.