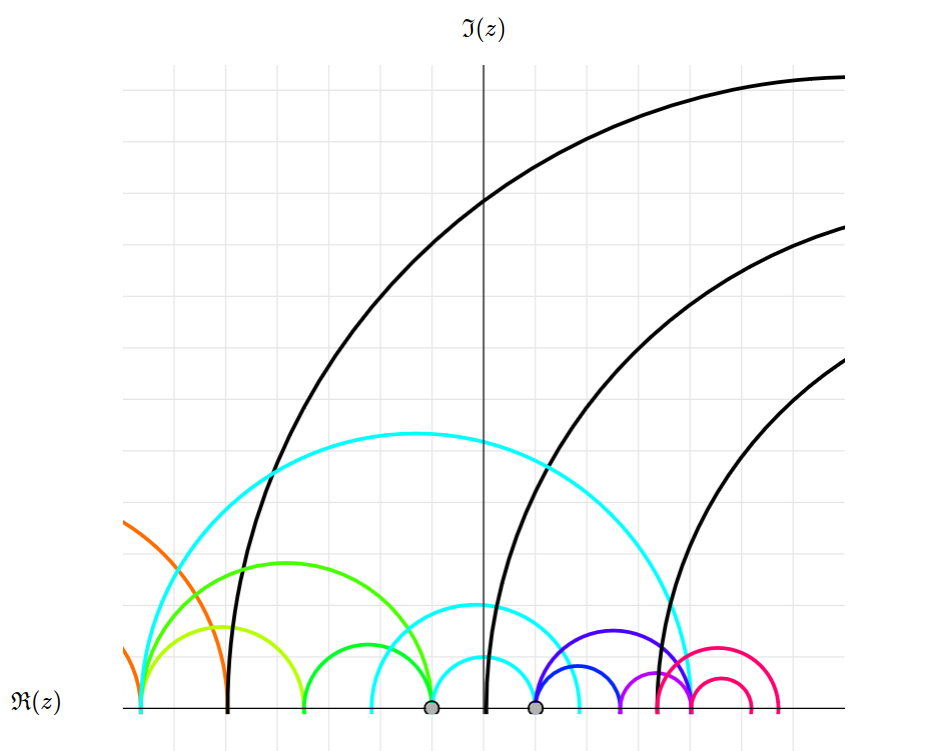
This website lets you visualize the action of \(\mathrm{PSL}(2,\mathbb{R})\) on \(\mathbb{H}_{\mathrm{sup}} \coloneqq \{x+iy \in \mathbb{C} : y>0\}\), the upper half-plane or Poincaré half-plane model. The action is a Möbius transformation, meaning that the action is defined by \[\begin{pmatrix}a&b\\c&d\end{pmatrix}\cdot z = \frac{az+b}{cz+d},\] where \(z \in \mathbb{H}_{\mathrm{sup}}\) and \(a,b,c,d \in \mathbb{R}\) are such that \(ad-bc=1\).
The functioning of the program is based on the following theorem:
Classification of isometries. \(\mathrm{PSL}(2,\mathbb{R})\) is the group of orientation-preserving isometries of \(\mathbb{H}_{\mathrm{sup}}\).
Furthermore, a transformation satisfies exactly one of these cases:
The program uses the fact that, given one of these situations, there exists a unique transformation that maps \(z_{1} \in \mathbb{H}_{\mathrm{sup}}\) to \(z_{2} \in \mathbb{H}_{\mathrm{sup}}\) or \(x_{1} \in \mathbb{R}\cup\{\infty\}\) to \(x_{2} \in \mathbb{R}\cup\{\infty\}\), depending of the case. The grey points represent the fixed points. By dragging your mouse, you specify \(z_{1} \mapsto z_{2}\) or \(x_{1} \mapsto x_{2}\). The program differentiates these cases for you. Then, it finds the unique transformation and applies it to the hyperbolic lines!
This website is greatly inspired by the one made to visualize the action of \(\mathrm{PSP}(4,\mathbb{R})\) on the Riemann sphere. The code relating to this website is on GitHub. The visualizations were made using CindyJS.